
Головоломка «Квадрат» | Блог 4brain
Головоломка «Квадрат» — это простая и понятная флеш-игра для тренировки интеллектуальных навыков online, которая подойдет как взрослым, так и детям. В игре 9 уровней объединенных в 3 блока в соответствии с их архитектурой и сложностью.
В первых трех вам нужно выполнить условие на квадрате размером 5х5, в последующих трех – 6х6, и в уровнях 7-9 – на квадрате 7х7. Существует возможность перемещения между уровнями без обязательного прохождения предыдущего.
Правила игры. Задача игрока – зачеркнуть одной ломанной непрерывной линией все пустые ячейки квадрата. Линия начинается с места выбранного пользователем и чертится от стартовой позиции до любой преграды по вертикали и горизонтали (ею могут быть черный шар, границы игрового поля и граница линии проложенной ранее). Начало игры – клик на «Play», перезапуск уровня с начала – restart.
Поиск решения
Как и в случае с головоломкой «Найди путь» дать действенный алгоритм поиска решения не представляется возможным. Это своеобразная дополнительная мотивация разобраться с задачей эвристически, один на один.
Желаем успеха в решении головоломки!
Тренируемые навыки
В процессе тщательного размышления над построением маршрута тренируются следующие навыки:
- Пространственное мышление – вид умственной деятельности отвечающий за создание пространственных образов и оперирование ими в процессе решения практических и теоретических задач;
- Абстрактно-логическое мышление;
- Память.
Любите подобные загадки, игры, головоломки и тесты? Получите неограниченный доступ ко всем интерактивным материалам на сайте, чтобы развиваться эффективнее.
Отзывы и комментарии
Оцените головоломку и поделитесь своими достижениями в ее прохождении – оставьте комментарий, воспользовавшись специальной формой под этой статьей.
4brain.ruПроектная работа по математике «Удивительный квадрат»
Иркутская область
Усольский район
муниципальное бюджетное общеобразовательное учреждение «Раздольинская СОШ»
подразделение
Проектная работа
«Удивительный квадрат»
Сведения об авторе:
Милоградова Алёна Алексеевна
СП МБОУ «Раздольинская СОШ»
6 класс
Сведения о руководителе:
Трухина Ольга Степановна
учитель математики
СП МБОУ «Раздольинская СОШ»
п. Октябрьский, 2016
Оглавление:
1. Введение
2. Основная часть
2.1. Решение задач – головоломок
2.2. Легенды возникновения игры «Танграм»
2.3. Игра «Танграм»
3. Заключение
4. Литература
5. Приложение 1. Зачет «Танграм»
6. Приложение 2. Ответы к головоломкам
Введение
Из исторических источников известно, что древние египтяне и китайцы знали такую геометрическую фигуру как квадрат. Интерес к квадрату объясняется его свойствами, широко используемые в практике: измерение площадей земельных участков, определение расстояния до объекта, в технике архитектурных сооружений и т.д. Современные математики, продолжая традиции древних, не отрывают науку от практики, глубоко разрабатывают ее прикладные стороны. Известно много примеров огромной экономии за счет продуманного изменения раскроя промышленных материалов.
Существует множество геометрических задач, которые невозможно решить, пользуясь только линейкой и циркулем. Поэтому были изобретены методы решения с помощью не традиционных инструментов. Так было предложено выполнять построения перегибанием квадратного листа. Аналогичные построения можно осуществлять и методом разрезания квадрата. На основе этого были придуманы разные головоломки, которые очень популярны среди любителей занимательной математики.
Квадрат – это удивительная фигура, имеющая определенные свойства, которые в школьном курсе геометрии даны поверхностно.
Цель моей работы заключается в изучении игр головоломок, связанных с квадратами.
Для достижения цели я поставила перед собой следующие задачи:
1) научиться решать головоломки из квадратов, разрезанных на
несколько частей;
2) ознакомиться с историей возникновения игры «Танграм»;
3) решить задачи — головоломки, предложенные в разных источниках;
4) составить свои картинки – силуэты из чёрного квадрата Та-нга.
Практическое значение моей работы в том, что её можно будет использовать, как дополнительный материал на уроках геометрии. Конструирование фигур из полученных частей является не только полезной геометрической забавой, но имеет и практический смысл: они могут помочь будущим и настоящим новаторам производства в рациональном раскрое материала, в использовании обрезков кожи, ткани, дерева и т.д., для превращения их в полезные вещи. Игру «Танграм» — можно использовать как одну из форм проверки знаний учащихся, которая в занимательной форме требует проявления таких качеств личности как умение взаимодействовать в группе, сообразительность, проявление волевых усилий в достижении поставленной цели. Она даёт каждому ученику опыт совместной с партнёром деятельности, ощущение значимости своего вклада в общее дело. Игру «Танграм» я предлагаю провести в 7 классе по теме «Графики линейной функции» (Приложение №1).
Решение задач – головоломок
Составление всевозможных фигур из квадрата остается актуальным и сегодня. В умелых руках самый обыкновенный квадрат становится удивительной геометрической фигурой. Он может, например, весь без остатка превратиться в другую фигуру или в несколько других фигур правильной или неправильной формы. Но для каждого превращения квадрат предварительно должен быть разрезан на отдельные части.
Задачи на разрезания считаются одними из самых увлекательных головоломок в занимательной математике. Многие из задач на разрезание правильных фигур очень красивы, так как наглядно демонстрируют четкие связи между формами и размерами этих фигур, обусловленные их симметрией. В этих задачах требуется разрезать данную плоскую фигуру на части, из которых можно сложить другую, уже заданную плоскую фигуру так, чтобы обе фигуры были равносоставленными, то есть состояли из не перекрывающихся частей без свободных промежутков. При этом очень важно, чтобы число частей было как можно меньше, так как строго доказано, что любой многоугольник можно, разрезав на конечное число частей, преобразовать в любой другой многоугольник, равновеликий исходному (т.е. многоугольники должны иметь равные площади).
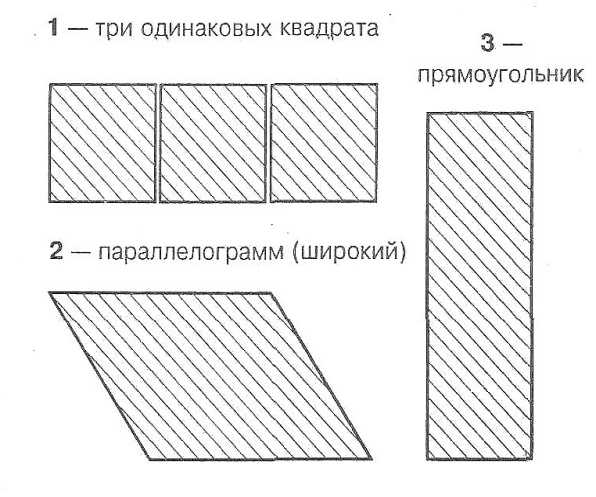
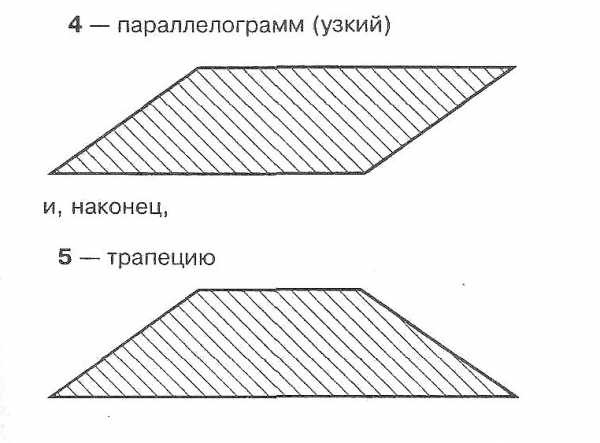
Задача №1. Из семи частей квадрата №1 составьте:
Три одинаковых квадрата.
Прямоугольник.
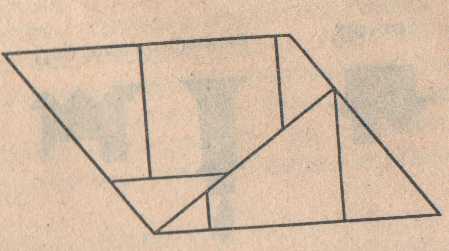
Параллелограмм (широкий)
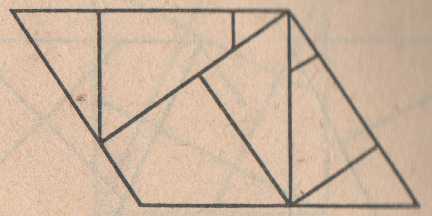
Параллелограмм (узкий)
Трапецию.
Задача №2. Из восьми частей квадрата №2 составьте:
Параллелограмм.
Три квадрата.
Из частей квадрата а) и в) составить прямоугольник и другой квадрат.
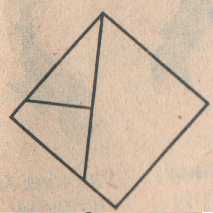
Задача №3. Из квадрата №3 составьте равнобедренный треугольник.
Задача №4. Из квадрата №4 составьте прямоугольный треугольник.
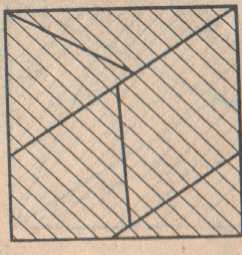
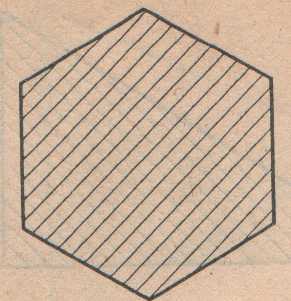
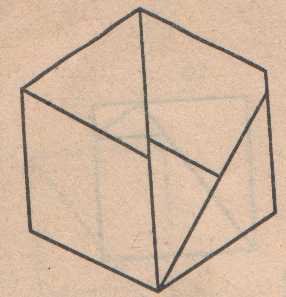
Задача №5. Из квадрата №5 составьте правильный шестиугольник.
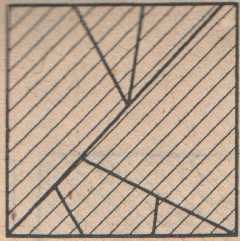
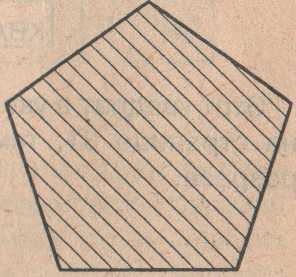
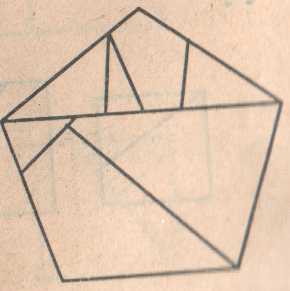
Задача №6. Из квадрата №6 составьте правильный пятиугольник.
Задача №7. Из квадрата №7 составьте равносторонний треугольник, а затем прямоугольник.
Задача №8. Очень остроумно разрезал квадрат №8 ещё несколько тысяч лет тому назад китайский ученый Та-нг. Вероятно, эти части квадрата первоначально служили для демонстрации геометрических фигур. С течением времени было замечено, что из этих частей можно составить множество фигур-силуэтов самой причудливой формы, употребляя для составления каждой фигуры все семь частей квадрата.
Ответы к головоломкам даны в приложении №2.
Квадрат №1.
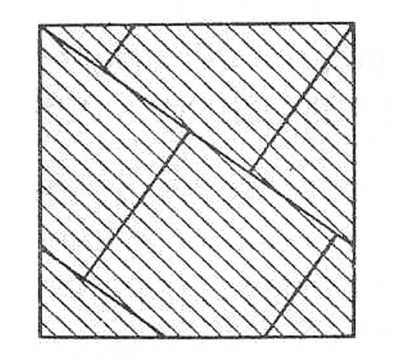
Из семи частей квадрата №1 составьте:
Квадрат №2

Из его восьми частей можно сделать такой же параллелограмм, как в головоломке 2
6.
Квадрат можно превратить в три квадрата, площади которых относятся как 2:3:4
7. 8. 9.
В свою очередь, из частей двух квадратов a и в можно составить один квадрат или прямоугольник.
10. 11.
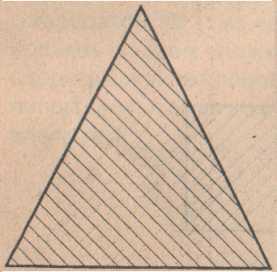
Квадрат №3
Превратите квадрат №3 в равнобедренный треугольник
 12.
12. 
Превратите квадрат №4 в прямоугольный треугольник
 13.
13.
Квадрат №5
Из пяти частей этого квадрата составьте правильный шестиугольник.
 14.
14.
Квадрат №6
Из семи частей квадрата составьте правильный пятиугольник.
 15.
15. 
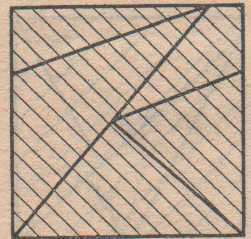
Квадрат №7
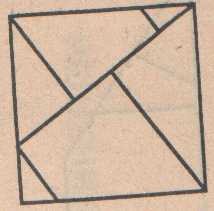
Превратите квадрат № 7 в равносторонний треугольник, а затем в прямоугольник.
 16. 17.
16. 17.
Квадрат №8
Но особый интерес представляет черный квадрат Та-нга

Вот некоторые из них:


До появления компьютерных игр и бурного развития настольных, одним из основных развлечений для большинства детей и множества взрослых была игра — головоломка «Тан-грам». Базовым элементом танг-рама являются таны, которые получают при разрезании квадрата на семь геометрических фигур. Из них можно сложить большое количество различных фигур (животные, птицы, орудия труда, мебель, предметы быта и т.д.). Игра помогает развивать логическое мышление, геометрическую интуицию.
Буквально слово тан-грам означает «семь дощечек мастерства». Это головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.).
Легенды возникновения игры “Танграм”.
Легенда первая: более 4 тысяч лет назад у одного человека выпала из рук фарфоровая плитка и разбилась на семь частей. Расстроенный, он в спешке старался ее сложить, но каждый раз получал новые интересные изображения. Это занятие оказалось настолько увлекательным, что впоследствии квадрат, составленный из семи геометрических фигур, назвали Доской Мудрости.
Легенда вторая: это было очень давно, почти две с половиной тысячи лет тому назад. У немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого императора: его сын, будущий властелин огромной страны, не хотел учиться. Мальчику доставляло огромное удовольствие целый день забавляться игрушками. Император призвал к себе трёх мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. И три мудреца придумали эту игру. Говорят, что это была любимая игра Наполеона.
Легенда третья: местом, где была изобретена игра, несомненно, является Китай. Дата создания может быть определенна приблизительно XVIII век. Первой известной древней книгой по танграму является “Собрание фигур из семи частей” (Китай 1803 г.). Издана она была на рисовой бумаге. Книги, изданные в Европе, были лишь отчасти оригинальны, а в своей основе имели китайские источники.
“В записках покойного профессора Челленора, попавших в руки автора, — утверждал Лойд, — имеются сведения о том, что семь книг о танграмах, каждая из которых насчитывает ровно тысячу фигур, были составлены в Китае более 4000 лет назад. Эти книги ныне стали столь большой редкостью, что за те сорок лет, которые профессор Челленор провел в Китае, ему лишь раз удалось видеть первое издание первого из семи томов (сохранившихся полностью) и несколько разрозненных фрагмента второго тома.
В этой книге связи уместно напомнить, что части одной из книг, напечатанной золотом на пергаменте, были обнаружены в Пекине английским солдатом, продавшим свою находку за 300 фунтов стерлингов одному собирателю китайской старины, который любезно предоставил некоторые наиболее изысканные фигурки для воспроизведения в этой книге”.
Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству. Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа “инь и ян”. Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудию труда, мебель, одежда и архитектурные сооружения. Лойд часто цитирует высказывания Конфуция, философа по имени Шуфуце, комментатора Ли Хуанчжан и вымышленного профессора Челленора. Ли Хуанчжан упоминается в связи с тем, что по преданию он знал все фигуры из семи книг Тана прежде, чем научился говорить. Встречаются у Лойда и ссылки на “известные” китайские пословицы типа «Только глупец взялся бы написать восьмую книгу Тана».
Правила игры «Танграм».
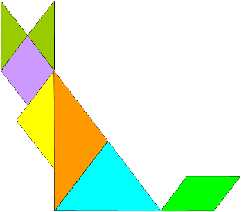
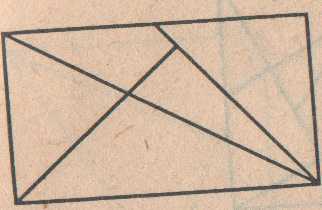
Для игры квадрат разрезается на семь частей так, как показано на рисунке. При этом получаются два больших равных треугольника, один средний и два маленьких равных треугольника, один квадрат и один параллелограмм. Минимальное количество базовых фигур, равное семи, приводит к гениальной простоте комбинаций. Суть игры заключается в конструировании на плоскости разнообразных предметных силуэтов. Многообразие и различная степень сложности геометрических конструкторов позволяет учитывать возрастные особенности детей, их склонности, возможности, уровень подготовки. Все собираемые фигуры должны иметь равную площадь, так как собираются из одинаковых элементов. Отсюда следует, что: 1)в каждую собираемую фигуру должны войти непременно все семь элементов; 2)при составлении фигуры элементы не должны налегать друг на друга, то есть располагаются только в одной плоскости; 3)элементы фигур должны примыкать один к другому.
Познакомившись с задачами-головоломками, я решила использовать некоторые квадраты для составления фигур. Придумала их самостоятельно.



Заключение
В результате проведённой работы по теме «Удивительный квадрат» изучена математическая литература и сделан ряд выводов.
1) Квадрат — это неисчерпаемая фигура, применяемая во многих сферах и имеющая свойства, интересные для каждого, кто стремится расширить рамки своих геометрических представлений.
2) Существуют занимательные игры, в которых используется квадрат.
3) Моя работа может заинтересовать учащихся, ее могут использовать учителя при проведении математических конкурсов, для организации игровых моментов на уроке.
4) Упражнения с разрезанием квадрата и конструированием фигур из полученных частей является не только полезной геометрической забавой, но имеют и практический смысл: они могут помочь будущим и настоящим новаторам производства, в рациональном раскрое материала, в использовании обрезков кожи, ткани, дерева и т.д., для превращения их в полезные вещи.
Я разобрала лишь одну из замечательных головоломок. Танграм может применяться на уроках математики для получения начальных сведений о геометрии. Знакомство с простейшими геометрическими фигурами: квадрат, треугольник, ромб, знакомство с углами. Сравнение фигур по форме, размеру, площади. Составление из нескольких фигур новой геометрической фигуры. Играя, мы запоминаем названия геометрических фигур, их свойства, отличительные признаки, обследуем формы зрительным и осязательно-двигательным путем, свободно перемещаем их с целью получения новой фигуры. У нас развивается умение анализировать простые изображения, выделять в них и в окружающих предметах геометрические формы, практически видоизменять фигуры путем разрезания и составлять их из частей. Исследовав практическое применение «Танграма», я пришла к выводу, что комбинируя на плоскости элементы разрезанного на части квадрата, можно создавать множество новых фигур, как геометрических, так и жанровых — очертания животных, людей, бытовых предметов и т.д. Эта головоломка развивает умственные и творческие способности, пространственное воображение, комбинаторные способности, логическое мышление, сообразительность, смекалку, а также усидчивость и мелкую моторику, формирует внимательность, упорство в достижении цели, способствует творческому поиску чего – то нового, учит терпению и последовательности.
Мною проведен урок в начальных классах, на котором я познакомила ребят с этой чудесной головоломкой «Танграм», показала какие можно составить фигурки из черного квадрата и помогла сделать аппликацию.

Литература:
1. Гарднер М., Математические головоломки и развлечения. – М.: Оникс,
1994.
2. Депман И.Я., Виленкин Н.Я. За страницами учебника математики,
Москва, «Просвещение», 1989.
3. Игнатьев Е.И., «В царстве смекалки». Москва, «Наука», 1978.
4. Леман И. «Увлекательная математика». Москва, «Наука», 1978.
5. Кордемский Б.А., Русалев Н.В. Удивительный квадрат – М.: АО
«Столетие», 1994.
6. Кордемский Б.А., «Математическая смекалка», Санкт-Петербург,
«Манускрипт», 1994.
7. Перельман Я.И., «Занимательная геометрия», Москва, издательство
«АСТ», 2003.
8. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия, 5-6 кл: учебное
пособие. Москва: Дрофа, 1998.
Приложение № 1
Зачет «Танграм»
Методика проведения: учащиеся делятся на группы. Каждая группа получает задание разработать макет детской игрушки с заданными параметрами. Эти параметры – функции, графики которых надо построить в одной системе координат. При построении графиков получаются контуры игрушки и они должны с помощью полученных каждой группой танов сложить эти контуры. Все таны должны быть задействованы. Нельзя накладывать их друг на друга.
«Гусь»
у = х + 19, -8 < х < 0;
х = 0, 16 < у < 19;
у = —х + 16, 0 < х < 4;
х = 4, 4 < у < 12;
у = —х + 8, 4 < х < 16;
у = х – 24, 3 < х < 16;
х = 8, -16 < у < —8;
у = х – 16, 0 < х < 8;
х = 0, -16 < у < 11;
у = 11, -8 < х < 0.
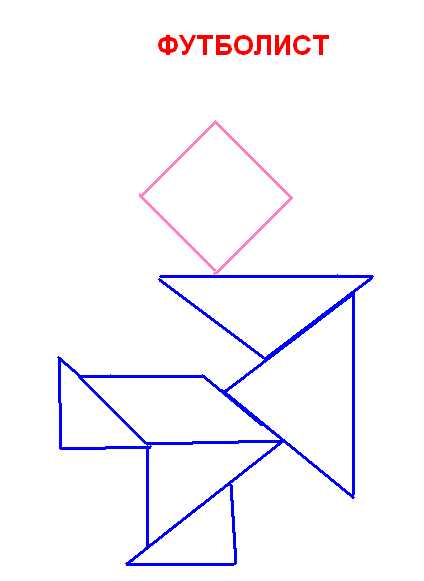
«Футболист»
у = 2,5х + 21, -2 < х < 0;
у = -2/5х + 21, 0 < х < 5;
у = 2.5х + 6.5, 3 < х < 5;
у = 14, 3 < х < 12;
у = х + 2, 9 < х < 12;
х = 9, -5 < у < 11;
у = -х + 4, 6 < х < 9;
у = х – 8 , 1 < х < 6;
у = х = 1, -13 < х < —7;
у = х –13, -5 < х < 1;
у = х – 8, -5 < х < —2;
х = -2, -10 < у < —2;
у = -2, -2 < х < 0;
14) у = —х -2, -2 < х< 0;

15) у = 0, -8 < х < -2;
16) х = -8, 0 < у < 6;
17) -8 < х < —6, у = —х -2;
18) у = 4, -6 < х < 0;
19) у = —х + 4, 0 < х < 1;
20) у = х + 2, 1 < х < 4;
21) у = —х + 10, -4 < х < 4;
22) у = 14, -4 < х < 3.
Приложение № 2
Ответы к головоломкам
1.


2.
 3.
3.4.
5.
6.

7, 8, 9.
10.
 11.
11.12. 13. 14. 15.




16.
 17.
17. 
infourok.ru
Головоломка «Сложи квадрат» — Наши поделки, игрушки своими руками, игры — Блог «В гостях у Весны»
Ура, ура, ура! Я наконец-то доделала игру — головоломку «Сложи квадрат» по методике Никитиных.
Подробнее о ней можно почитать на сайте семьи Никитиных.
Суть игры в том, чтобы из небольших частей разной формы сложить квадрат. Сначала собираем квадраты из двух и трех частей. Потом уже из четырех, пяти и т.д. То есть идем от простого к сложному. Каждый квадрат отличается по цвету. Игра развивает сообразительность, пространственное воображение, логическое мышление, математические и творческие способности, цветовосприятие. Я думаю, что игра увлекательна не только для детей, но и для взрослых. И некоторые квадратики довольно-таки сложно собрать даже взрослым. Мы играем с удовольствием в эту игру всей семьей. 😉
Эту игру можно приобрести в магазинах, но можно сделать и самостоятельно из фанеры, картона, линолеума или др. подручных материалов.
Вот процесс изготовления:

Как видите, все просто. Я сделала из картона рамочку (даже две) и много квадратиков. Каждый размером примерно 8х8 см. Квадратики обклеила с одной стороны цветной бумагой, каждый разного цвета. Рамочку обклеила цветным скотчем. Вот такая рамка в итоге получилась:

Игра «Сложи квадрат», которая есть в магазинах, тоже в рамочке. Но на сайте Никитиных ни о какой рамочке речи нет. И действительно, без рамки квадраты составлять гораздо сложнее, рамка облегчает эту задачу. Многие родители, создавая самостоятельно эту игру, отказываются от рамок именно по этой причине. Но я решила все-таки сделать рамочку, пусть будет)) А собирать квадратики как с ней, так и без нее, что мы и делаем.
На упомянутом сайте Никитиных есть схемы квадратов, но можно подойти к этому делу творчески и создать свои)
После того, как я обклеила картонные квадраты цветной бумагой и они высохли, я разметила квадраты карандашом на части и затем разрезала их по линиям. Я написала номер квадрата на каждой его части с обратной стороны, чтобы потом не перепутать части (некоторые квадраты у меня одинаковых цветов). А затем обклеила части скотчем, чтобы дольше сохранились.
Вот такие квадраты у меня получились.
Самые простые в сборке:

Черный квадрат не разрезан. Остальные состоят из двух или трех частей. С этими квадратами дочка справляется с легкостью как в рамочке, так и без нее.
Второй уровень сложности:
Здесь уже квадратики состоят из трех, четырех и даже пяти частей. На этом уровне сложности дочке пока не удается собрать три квадратика. А те, которые она собирает, в рамке собираются с большим успехом, чем без нее. Но мы пробуем и так, и так.
Следующий уровень сложности:
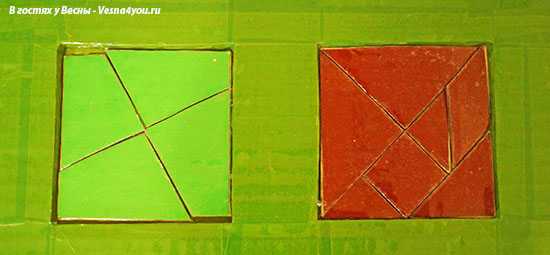
Здесь у дочки тоже некоторые квадратики получается собрать, некоторые пока еще нет.
И еще два квадратика:
Квадраты, кроме последнего коричневого, я делала по схемам, приведенным на сайте Никитиных. Но я сделала пока не все предложенные варианты, а сколько можно еще придумать! Квадраты каждого уровня сложности я храню в отдельных файлах.
Как мы играем в квадраты?

1) Я даю дочке файл с частями квадратов одного уровня сложности. Ей предстоит решить несколько задач. Во-первых, разложить все части по цветам. Потом уже попытаться собрать квадратики из элементов одного цвета. Как я уже писала, собираем и без рамки, и в рамке. Параллельно можно изучать, из каких фигурок состоит квадрат.
2) Можно поиграть в игру, предложенную на сайте Никитиных, а именно: построить дорожку для кукол из квадратиков. Достаем первый квадратик целый, ребенок складывает. А следующий квадратик уже состоит из нескольких частей. Можно придумать целую историю: «Ой, кто-то разрезал квадратик. Что же нам теперь делать?». Мало того, что ребенку нужно составить квадрат из частей, но еще и ровно приложить его к предыдущему квадрату. Так и выстраиваем дорожку. А потом куколки шагают по ней 😉
Помимо дорожки можно придумать и другие сюжеты игр, например, построить квадратные домики, полянки и т.д.
3) А можно из частей квадратиков предложить составить какие-нибудь фигурки, конструировать: елочки, домики, кораблики, животных и т.д. Как по заданному примеру, так и позволив творить самостоятельно.

4) Можно предложить ребенку найти и выбрать все треугольники, четырехугольники и т.д.
5) Можно предложить разложить все части квадратов по их размеру: от самых маленьких к большим.
6) Для тех, кто уже начинает изучать цифры, можно дать задание сортировать части квадратов не только по цветам, но и по цифрам, подписанным на обороте каждой части.
Отдельно хочется остановиться на последнем нашем коричневом квадратике. Это танграм.

Танграм — это довольно известная самостоятельная головоломка, которая представляет из себя квадрат, разрезанный на 7 частей: 2 больших треугольника, 1 средний, 2 маленьких, квадрат и параллелограмм. Суть игры «Танграм» — собрать из ее частей какую-нибудь фигурку: человека, животных и др. Существует множество различных комбинаций.
Вот, к примеру, такие:


Будем пробовать составлять. 😉
Танграм можно приобрести в магазинах. Например, в Озоне — магнитный танграм от Djeсo. В Май-шопе — разноцветный танграм с деревянной основой, скоростной танграм (с 4 наборами танграм).
Слайд-шоу из фотографий игры — головоломки «Сложи квадрат»:
До новых встреч!
Антонина Ефимова Весна,
автор блога «В гостях у Весны»
P.S. Мне будет приятно, если вы выразите свое мнение о прочитанной статье. Это можно сделать тремя способами:
1) Оставьте комментарий. Форма комментариев располагается ниже. Мне приятно общаться со своими читателями. 🙂
2) Поделитесь статьей в социальных сетях.
3) Оцените статью, нажав на звездочки ниже статьи.
vesna4you.ru
Как работает магический квадрат?
Данная загадка быстро разлетелась по всему Интернету. Тысячи людей начали задаваться вопросом о том, как работает магический квадрат. Сегодня вы, наконец-то, найдете ответ!
Тайна магического квадрата
На самом деле данная загадка довольно проста и сделана с расчётом на человеческую невнимательность. Давайте разберемся, как работает магический черный квадрат, на реальном примере:
- Давайте загадаем любое число от 10 до 19. Теперь давайте вычтем из данного числа его составляющие цифры. К примеру, возьмем 11. Отнимем от 11 единицу и после – еще одну единицу. Выйдет 9. На самом деле не важно, какое число от 10 до 19 вы возьмете. Результат вычислений всегда будет 9. Числу 9 в «Магическом Квадрате» соответствует первая цифра с рисунками. Если присмотреться, то можно увидеть, что очень большому количеству цифр присвоены одни и те же рисунки.
- Что же будет, если взять число в пределах от 20 и до 29? Может, вы уже сами догадались? Правильно! Результатом вычислений всегда будет 18. Цифра 18 соответствует второй позиции на диагонали с рисунками.
- Если же взять число от 30 до 39, то, как можно уже угадать, выйдет число 27. Число 27 также соответствует цифре на диагонали столь необъяснимого «Магического Квадрата».
- Подобный алгоритм остается правдивым для любых чисел от 40 до 49, от 50 до 59 и так далее.
То есть выходит, что неважно, какое число вы загадали — «Магический Квадрат» угадает результат, ведь в клетках под номерами 9, 18, 27, 36, 45, 54, 63, 72 и 81 на самом деле находится один и тот же символ.
На самом деле данную загадку можно легко объяснить с помощью простого уравнения:
- Вообразите любое двухзначное число. В независимости от числа его можно представить в виде x*10+y. Десятки выступают в роли “x”, а единицы в роли “у”.
- Вычтите из загаданного числа цифры, которые составляют его. Складываем уравнение: (x*10+y)-(x+y)=9*x.
- Число,
elhow.ru


 3.
3.
 11.
11.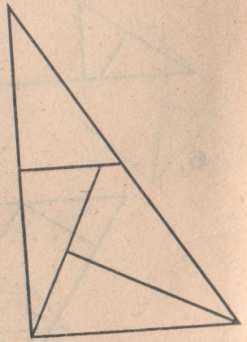

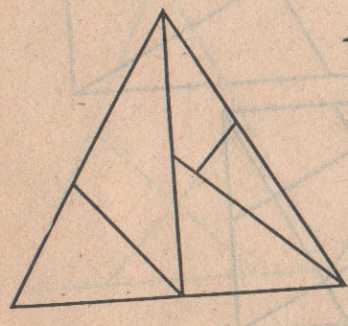 17.
17. 
Оставить комментарий